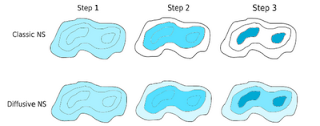
Brendon et. al. has a newer version of nested sampling algorithm, they call it Diffusive Nested Sampling (DNS). As the name indicates, it principally differs from the "classic" nested sampling in presenting the hard constraint. It relaxes the hard evolving constraint and lets the samples to explore the mixture distribution of nested probability distributions, each successive distribution occupying e^-1 times the enclosed prior mass of the previously seen distributions. The mixture distribution is weighted at will (a hack :P) which is a clever trick of exploration. This reinforces the idea of "no peaks left behind" for multimodal problems.
On a test problem they claim that DNS "can achieve four times the accuracy of classic Nested Sampling, for the same computational effort; equivalent to a factor of 16 speedup".
PS:
What can grow out of side talks in a conference?
If you know the power of scrapping in the napkin paper, you would not be surprised.
The paper is available in arxiv:
http://arxiv.org/abs/0912.2380
The code is available at: http://lindor.physics.ucsb.edu/DNest/; comes with handy instructions.
---
Thanks are due to Dr. Brewer for indicating typos in the draft and suggestions + allowing to use the figures.
The original nested sampling code is available in the book by sivia and skilling: Data Analysis: A Bayesian Tutorial


Edit: Sep 5, 2013
An illustrative animation of Diffusive Nested Sampling (www.github.com/eggplantbren/DNest3) sampling a multimodal posterior distribution. The size of the yellow circle indicates the importance weight. The method can travel between the modes because the target distribution includes the (uniform) prior as a mixture component.
On a test problem they claim that DNS "can achieve four times the accuracy of classic Nested Sampling, for the same computational effort; equivalent to a factor of 16 speedup".
I have not played with it yet. However, it seems worth trying. Just a note to myself.
PS:
What can grow out of side talks in a conference?
If you know the power of scrapping in the napkin paper, you would not be surprised.
The paper is available in arxiv:
http://arxiv.org/abs/0912.2380
The code is available at: http://lindor.physics.ucsb.edu/DNest/; comes with handy instructions.
---
Thanks are due to Dr. Brewer for indicating typos in the draft and suggestions + allowing to use the figures.
The original nested sampling code is available in the book by sivia and skilling: Data Analysis: A Bayesian Tutorial